Conectar modelos¶

Ejemplo muy básico¶

Empezaremos con un modelo bastante sencillo. Pero demuestra muy bien cómo funciona Tinamït, y no tienes que instalar cualquier modelo biofísico externo para que te funcione, así que empecemos con este.

Primero vamos a utilizar este modelo de dinámicas de sistemas:

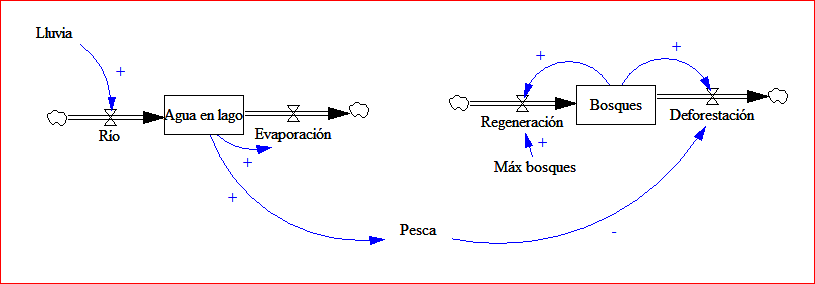
El modelo DS determina, dado la lluvia, la cantidad de pesca posible y su impacto en la necesidad de explotar recursos del bosque.

Del otro lado, el «modelo» biofísico nos da la precipitación según la cubertura forestal.

import matplotlib.pyplot as plt

from tinamit.conect import Conectado
from tinamit.ejemplos import obt_ejemplo

mds = obt_ejemplo('sencillo/mds_bosques.mdl')
bf = obt_ejemplo('sencillo/bf_bosques.py')

modelo = Conectado(bf=bf, mds=mds)

# Vamos a conectar los variables necesarios
modelo.conectar(var_mds='Lluvia', var_bf='Lluvia', mds_fuente=False)
modelo.conectar(var_mds='Bosques', var_bf='Bosques', mds_fuente=True)

# Y simulamos
res_conex = modelo.simular(200)

# Visualizar
f, (eje1, eje2) = plt.subplots(1, 2)
eje1.plot(res_conex['mds']['Bosques'].vals)
eje1.set_title('Bosques')
eje1.set_xlabel('Meses')

eje2.plot(res_conex['mds']['Lluvia'].vals)
eje2.set_title('Lluvia')
eje2.set_xlabel('Meses')

eje1.ticklabel_format(axis='y', style='sci', scilimits=(0,0))

(Source code, png, hires.png, pdf)

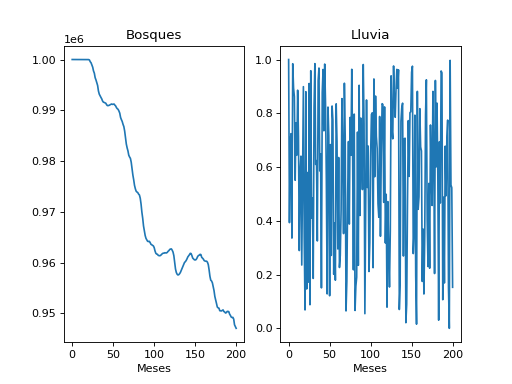
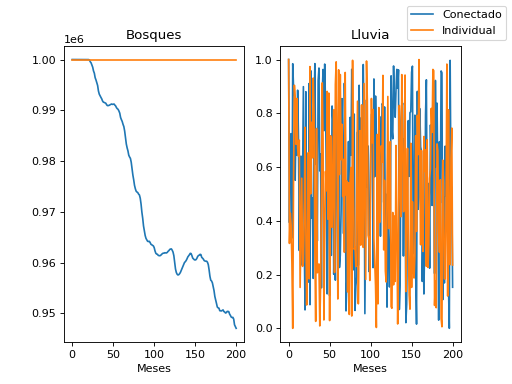
Tambiém comparemos a una corrida sin conexión para ver el impacto de incluir las relaciones entre ambiente y humano.

Nota

Siendo subclases de Modelo, modelos BF (ModeloBF) y DS (ModeloDS) también se pueden simular de manera independiente.

from tinamit.envolt.mds import gen_mds
from tinamit.envolt.bf import gen_bf

res_mds = gen_mds(mds).simular(200, nombre='Corrida_MDS')
res_bf = gen_bf(bf).simular(200, nombre='Corrida_BF')

# Visualizar
f, (eje1, eje2) = plt.subplots(1, 2)
eje1.plot(res_conex['mds']['Bosques'].vals, label='Conectado')
eje1.plot(res_mds['Bosques'].vals, label='Individual')
eje1.set_title('Bosques')
eje1.set_xlabel('Meses')

eje1.ticklabel_format(axis='y', style='sci', scilimits=(0,0))

eje2.plot(res_conex['mds']['Lluvia'].vals)
eje2.plot(res_bf['Lluvia'].vals)
eje2.set_title('Lluvia')
eje2.set_xlabel('Meses')

f.legend()

(Source code, png, hires.png, pdf)

Opciones de tiempo¶

Si quieres más control sobre los detalles del eje de tiempo, puedes pasar un objeto EspecTiempo a la función simular(). Allí puedes especificar no solo el número de paso sino también una fecha inicial (útil para corridas con datos o clima externo), el tamaño de cada paso, y la frequencia con cual se guardan los resultados.

from tinamit.tiempo import EspecTiempo

t = EspecTiempo(100, f_inic='2000-01-01', tmñ_paso=1, guardar_cada=1)
modelo.simular(t)

Unidades de tiempo¶

Tinamït se encargará de convertir entre unidades de tiempo para ti si difieren entre tus modelos. No obstante, si uno de tus modelos tiene unidad de tiempo no convencional o está en un idioma que Tinamït no reconoce, puede ser que tengas que especificar la conversión manualmente con nueva_unidad(), agregar_trad() o agregar_sinónimos().

from tinamit.unids import nueva_unidad, agregar_trad, agregar_sinónimos

# Una estación tiene 4 meses
nueva_unidad(unid='Estación', ref='Mes', conv=4)

# "día" se dice "நாள்" en Tamil
agregar_trad('día', 'நாள்', leng_trad='த', leng_orig='es', guardar=True)

# "தினம்" también quiere decir "día" en Tamil
agregar_sinónimos('நாள்', "தினம்", leng='த', guardar=True)

Tinamït reconoce las unidades de tiempo siguientes: año, mes, semana, día, hora, minuto, secundo, microsecundo, millisecundo, y nanosecundo.

3+ modelos¶

Si tienes más que 2 modelos para conectar, también es fácil con la clase SuperConectado. Se pueden conectar de manera horizontal o jerárquica, cómo prefieres.

Horizontal¶

Se pueden conectar modelos individuales de manera «horizontal» en un solo modelo SuperConectado.

from tinamit.conectado import SuperConectado

# Crear los 3 modelos
mod_1 = MiModelo1(nombre='modelo 1')
mod_2 = MiModelo2(nombre='modelo 2')
mod_3 = MiModelo3(nombre='modelo 3')

# El Conectado
conectado = SuperConectado([mod_1, mod_2, mod_3])

# Conectar variables entre dos de los modelos por el intermediario del tercero.
conectado.conectar_vars(
    var_fuente='Var 1', modelo_fuente='modelo 1', var_recip='Var 2', modelo_recip='modelo 2'
)
conectado.conectar_vars(
    var_fuente='Var 2', modelo_fuente='modelo 2', var_recip='Var 3', modelo_recip='modelo 3'
)

# Simular
res = conectado.simular(10, vars_interés=[mod_1.variables['Var 1'], mod_3.variables['Var 3']])

Los variables Var 1 del modelo 1 y Var 3 del modelo 3 ahora tendrán valores idénticos a través de la simulación.

Jerárquica¶

También se pueden anidar modelos adentro de otros.

# Los tres modelos
mod_1 = MiModelo1(nombre='modelo 1')
mod_2 = MiModelo2(nombre='modelo 2')
mod_3 = MiModelo3(nombre='modelo 3')

# El primer Conectado
conectado_sub = SuperConectado(nombre='sub', modelos=[mod_1, mod_2])
conectado_sub.conectar_vars(
    var_fuente='Var 1', modelo_fuente='modelo 1', var_recip='Var 2', modelo_recip='modelo 2'
)

# El segundo Conectado
conectado = SuperConectado([conectado_sub, mod_3])
conectado.conectar_vars(
    var_fuente=mod_2.variables['Var2'], var_recip='Var 3', modelo_recip='modelo 3'
)

# Correr la simulación
res = conectado.simular(10, vars_interés=[mod_1.variables['Var 1'], mod_3.variables['Var 3']])

Este código dará resultados idénticos a los del ejemplo horizontal arriba.